Учебные материалы Шарапова М.П.

Веб-сайт: http://sharapovmp.ru,

http://www.sharapovmp.ru

Перекатывающийся квадрат

© Шарапов Михаил Петрович, 2025

E-mail: autocad1012@yahoo.com

На подступах к тайнам делимости

Для самоподготовки по математике юного математика

Раздел 1

Обычная арифметика и геометрия

Задачи

Общее условие

Квадрат разделен на 4 клетки.

В каждую клетку вписана цифра 1, 2, 3 , 4, как показано на рисунке.

Квадрат перекатывают по прямой, как показано на рисунке.

При этом квадрат поворачивается каждый раз на 90⁰ по часовой стрелке вокруг своего нижнего правого угла.

Такой поворот назовем одним перекатыванием.

Когда клетки оказываются нижними, касающимися прямой, из цифр, записанных в этих клетках, составляется двузначное число.

Это число составляется по обычным правилам.

Левая цифра будет цифрой десятков.

Правая цифра будет цифрой единиц.

Получающиеся числа записывают подряд, начиная с исходного числа, образованного цифрами в клетках, которые были нижними до начала перекатываний.

Таким образом, каждое перекатывание добавляет 2 цифры к формируемому таким образом числу.

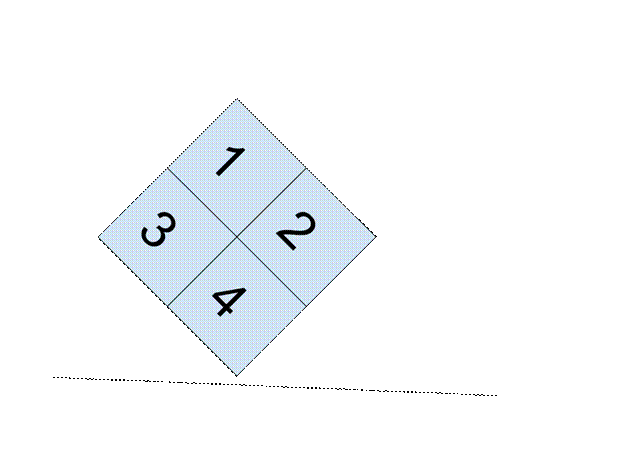
Рисунок 1

Задания

1

Докажите, что ни при каком начальном положении, ни при каком количестве перекатываний полученное число не будет делиться на 5.

2

Докажите, что ни при каком начальном положении, ни при каком количестве перекатываний полученное число не будет делиться на 4.

3

Если сначала нижними клетками были клетки с цифрами 34, какое наименьшее количество перекатываний позволит получить число, делящееся без остатка на 3?

4

Если сначала нижними клетками были клетки с цифрами 34, какое наименьшее количество перекатываний позволит получить число, делящееся без остатка на 9?

5

Если сначала нижними клетками были клетки с цифрами 34, какое наименьшее количество перекатываний позволит получить число, делящееся без остатка на 7?

6

Если сначала нижними клетками были клетки с цифрами 34, какое наименьшее количество перекатываний позволит получить число, делящееся без остатка на 11?

Раздел 2

Обычная арифметика и геометрия

Задачи

Общее условие

Квадрат разделен на 4 клетки.

В каждую клетку вписана цифра 1, 2, 3 , 4, как показано на рисунке.

Квадрат перекатывают по прямой, как показано на рисунке.

При этом квадрат поворачивается каждый раз на 90⁰ по часовой стрелке вокруг своего нижнего правого угла.

Такой поворот назовем одним перекатыванием.

Когда клетки оказываются нижними, касающимися прямой, из цифр, записанных в этих клетках, составляется двузначное число.

Это число составляется по обычным правилам.

Левая цифра будет цифрой десятков.

Правая цифра будет цифрой единиц.

Для каждого получаемого таким образом числа, находят остаток от деления этого числа на заданный делитель.

Эти остатки записывают подряд, начиная с остатка, полученного для исходного числа.

Назовем получаемое таким образом число – числом остатков для данного делителя.

Рисунок 2

Задания

7

Докажите, что ни при каком начальном положении, ни при каком количестве перекатываний полученное число остатков для делителя 5не будет делиться на 5.

8

Если сначала нижними клетками были клетки с цифрами 34, какое наименьшее количество перекатываний позволит получить число остатков для делителя 4, делящееся без остатка на 4?

9

Если сначала нижними клетками были клетки с цифрами 34, какое наименьшее количество перекатываний позволит получить число остатков для делителя 3, делящееся без остатка на 3?

10

Если сначала нижними клетками были клетки с цифрами 34, какое наименьшее количество перекатываний позволит получить число остатков для делителя 9, делящееся без остатка на 9?

11

Если сначала нижними клетками были клетки с цифрами 34, какое наименьшее количество перекатываний позволит получить число остатков для делителя 7, делящееся без остатка на 7?

12

Если сначала нижними клетками были клетки с цифрами 34, какое наименьшее количество перекатываний позволит получить число остатков для делителя 11, делящееся без остатка на 11?